| HARK version 1.1.0 Document |
This node performs Fast Fourier Transforms (FFT) on multichannel speech waveform data.
No files are required.
When to use
This node is used to convert multichannel speech waveform data into spectra and analyze the spectra with time frequency domains. It is often used as preprocessing of feature extractions for speech recognition.
Typical connection
Figure 6.82 shows an example, in which inputs of Matrix<float> and Map<int, ObjectRef> types are provided to the MultiFFT node. The path in Figure 6.82 receives multichannel acoustic signals of Matrix<float> type from the AudioStreamFromWave node. The signals are converted into Matrix<complex<float> > type complex spectra in the MultiFFT node and input to the LocalizeMUSIC node.
![\includegraphics[width=.8\textwidth ]{fig/modules/MultiFFT}](images/img-0770.png)
Parameter name |
Type |
Default value |
Unit |
Description |
LENGTH |
512 |
[pt] |
Length of signals to be Fourier transformed |
|
WINDOW |
CONJ |
Type of window function when performing Fourier transform. Select from CONJ, HAMMING and RECTANGLE, which indicate complex window, hamming window and rectangle window, respectively. |
||
WINDOW_LENGTH |
512 |
[pt] |
Length of window function when performing Fourier transform. |
Input
Matrix<float> or Map<int, ObjectRef> types. Multichannel speech waveform data. If the matrix size is 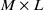 ,
, 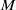 indicates the number of channels and
indicates the number of channels and 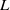 indicates the sample numbers of waveforms.
indicates the sample numbers of waveforms. 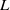 must be equal to the parameter LENGTH.
must be equal to the parameter LENGTH.
Output
Matrix<complex<float> > or Map<int, ObjectRef> types. Multichannel complex spectra corresponding to inputs. When the inputs are Matrix<float> type, the outputs are Matrix<complex<float> > type; when the inputs are Map<int, ObjectRef> type, the outputs are Map<int, ObjectRef> type. When the input matrix size is 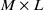 , the output matrix size is
, the output matrix size is 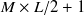 .
.
Parameter
int type. The default value is 512. Designate length of signals to be Fourier transformed. It must be expressed in powers of 2 to meet the properties of the algorithm. Moreover, it must be greater than WINDOW_LENGTH.
string type. The default value is CONJ. Select from CONJ, HAMMING and RECTANGLE, which indicate complex, hamming and rectangular windows, respectively. HAMMING windows are often used for audio signal analyses.
int type. The default value is 512. Designate the length of a window function. If this value increases, so does the frequency resolution, while the temporal resolution decreases. Intuitively, an increase in window length makes it more sensitive to differences in the pitch of sound while becoming less sensitive to changes in pitch.
Rough estimates of LENGTH and WINDOW_LENGTH It is appropriate to analyze audio signals with frame length of 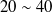 [ms]. If the sampling frequency is
[ms]. If the sampling frequency is 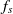 [Hz] and the temporal length of a window is
[Hz] and the temporal length of a window is  [ms], the frame length
[ms], the frame length 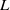 [pt] can be expressed as
[pt] can be expressed as
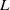 |
 |
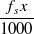 |
For example, if the sampling frequency is 16 [kHz], the default value 512 [pt] will correspond to 32 [ms]. Powers of 2 are suited for the parameter LENGTH of Fast Fourier Transform. Select 512. WINDOW_LENGTH, the window function, is set at 400 [pt], corresponding to 25 [ms] when the sampling frequency is 16 [kHz] in some cases to designate a frame length more suited for acoustic analyses.
Shape of each window function The shape of each window function 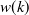 is defined by
is defined by 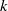 , the index of a sample;
, the index of a sample; 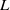 , the length of a window function; and
, the length of a window function; and 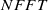 , the FFT length.
, the FFT length. 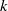 moves within a range of
moves within a range of 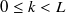 . When FFT length is greater than window length, the window function for
. When FFT length is greater than window length, the window function for 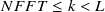 is 0.
is 0.
CONJ, Complex window
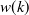 |
 |
![$\displaystyle \left\{ \begin{array}{cr} 0.5 - 0.5 \cos \frac{4kC}{L}, & \mathrm{if}\ \ 0 \leq k < L/4 \\ \undefined []{\left(1.5 - 0.5 \cos 2C-\frac{4kC}{L}\right) \left(0.5 + 0.5 \cos 2C-\frac{4kC}{L} \right)}, & \mathrm{if}\ \ L/4 \leq k < 2L/4 \\ \undefined []{\left(1.5 - 0.5 \cos \frac{4kC}{L}-2C\right) \left(0.5 + 0.5 \cos \frac{4kC}{L}-2C \right)}, & \mathrm{if}\ \ 2L/4 \leq k < 3L/4 \\ 0.5 - 0.5 \cos \left( 4C-\frac{4kC}{L} \right), & \mathrm{if}\ \ 3L/4 \leq k < L \\ 0, & \mathrm{if}\ \ NFFT \leq k < L \end{array} \right., $](images/img-0780.png) |
|||
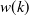 |
 |
![$\displaystyle \left\{ \begin{array}{cr} 0.5 - 0.5\cos \left( \frac{4k}{L}C \right), & \mathrm{if} 0 \leq k < L/4\\ \undefined []{1-\left\{ 0.5 - 0.5\cos \left(\frac{2L-4k}{L}C\right) \right\} ^2}, & \mathrm{if} L/4 \leq k < 2L/4\\ \undefined []{1-\left\{ 0.5 - 0.5\cos \left(\frac{4k-2L}{L}C \right) \right\} ^2}, & \mathrm{if} 2L/4 \leq k < 3L/4\\ 0.5-0.5\cos \left( \frac{4L-4k}{L}C\right), & \mathrm{if} 3L/4 \leq k < L\\ 0, & \mathrm{if} NFFT \leq k < L \end{array} \right., $](images/img-0782.png) |
Here, 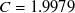 .
.
![\includegraphics[width=0.9\textwidth ]{fig/modules/MultiFFT_conj_time.eps}](images/img-0784.png)
![\includegraphics[width=0.9\textwidth ]{fig/modules/MultiFFT_conj_freq.eps}](images/img-0785.png)
Figures 6.83 and 6.84 show the shape and frequency responses of the complex window function. The horizontal axis in Figure 6.84 indicates the mean relative sampling frequency. Generally, frequency responses of a window function are better if the peak at 0 in the horizontal axis is sharper. Components outside the center of the frequency response indicate the amount of power of other frequency components that leak to a certain frequency bin when performing Fourier transformation. The vertical axis shows the power of other frequencies components that leak into a certain frequency bin when performing Fourier transformation.
HAMMING, Hamming window
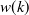 |
 |
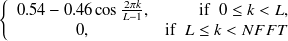 |
Here,  indicates a circular constant.
indicates a circular constant.
![\includegraphics[width=0.9\textwidth ]{fig/modules/MultiFFT_hamming_time.eps}](images/img-0787.png)
![\includegraphics[width=0.9\textwidth ]{fig/modules/MultiFFT_hamming_freq.eps}](images/img-0788.png)
Figures 6.85 and 6.85 show the shape and frequency responses of the hamming window function, respectively. RECTANGLE, Rectangle window
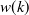 |
 |
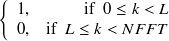 |
![\includegraphics[width=0.9\textwidth ]{fig/modules/MultiFFT_rect_time.eps}](images/img-0790.png)
![\includegraphics[width=0.9\textwidth ]{fig/modules/MultiFFT_rect_freq.eps}](images/img-0791.png)
Figures 6.87 and 6.87 show the shape and frequency responses of the rectangular window function, respectively.