SourceSeparation Node¶
Outline of the node¶
This node conducts blind sound source separation based on independent vector analysis.
Typical connection¶
The type of both the input and output of SourceSeparation node is multi-channel (2-ch) audio spectrum. Typical connection of this node is depicted as follows:
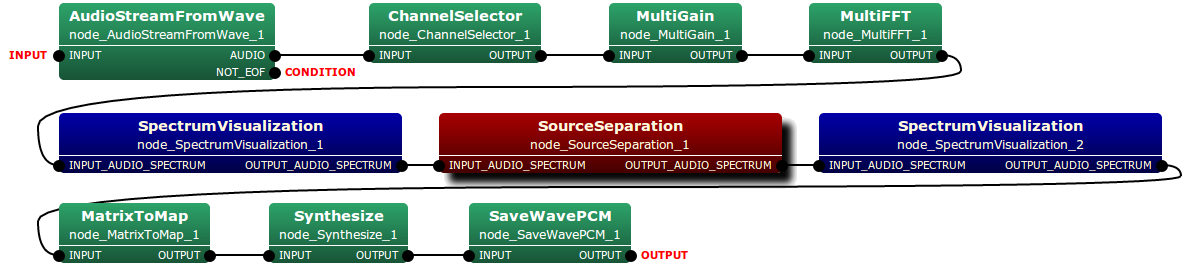
Input-output and property of the node¶
Input¶
- INPUT_AUDIO_SPECTRUM Matrix<complex<float> >
- Windowed spectrum data. A row index is channel, and a column index is frequency.
Output¶
- OUTPUT_AUDIO_SPECTRUM Matrix<complex<float> >
- Windowed and speech-enhanced spectrum data . A row index is channel, and a column index is frequency.
Parameters¶
Parameters of this node are listed as follows:
| Parameter name | Type | Default value | Unit | Description |
|---|---|---|---|---|
| FFT_LENGTH | int | 512 | sample | Analysis frame length. |
| ITERATION_METHOD | string | FastIVA | Iteration method. | |
| MAX_ITERATION | int | 700 | Processing limitation: maximum number of iterations. | |
| NUMBER_OF_SOURCE_TO_BE_SEPARATED | int | 2 | Number of sound sources to be separated. | |
| SEPARATION_TIME_LENGTH | float | 5.0 | second | Separation window length. |
| ADVANCE | int | 160 | sample | The length in sample between a frame and a previous frame. |
| SAMPLING_RATE | int | 16000 | Hz | Sampling rate. |
Details of the node¶
This module conducts recovery of the original sound signals from the combined sound signal by using independent vector analysis (IVA) [1] or Fast independent vector analysis (Fast-IVA) [2]. In the case of IVA, the objective function is Kullback-Leibler (KL) divergence:
\(C={\rm constant}- \sum^F_f {\rm log}\left|{\rm det} W_{mkf}\right| - \sum^M_m E\left[{\rm log}P \left( \hat{S}_1, \cdots ,\hat{S}_M \right)\right]\)
where \(\hat{S}_m (m = 1, \cdots, M)\) and \(W_{mkf}\) represent the input signal of m-th microphone and the separation matrix of IVA, respectively. The lerning algorithm of IVA is based on natural gradient-descent method:
\(W^{new}_{mkf}=W^{old}_{mkf} + \eta \sum^K_k \left( I_{mk} - E \left[ \frac{\hat{S}_{kf}}{\sqrt{\sum^F_f \left| \hat{S}_{kf} \right|^2}} \hat{S}_{kf}^{\ast} \right] \right) W^{old}_{mkf}\)
where \(\eta\) is learning rate (set at 0.1)
In the case of Fast-IVA, following modified objective function based KL divergence on is used:
\(C=-\sum^M_m E\left[{\rm log}P \left( \hat{S}_1, \cdots ,\hat{S}_M \right)\right] - \sum^M_m \beta\left[W^T_{mkf}W^{new}_{mkf}-1\right]\),
where \(\beta\) is Langrangian multiplier. The learning algorithm, on the other hand, is based on newton method with fixed point iteration:
\(W^{new}_{mkf}= E\left[\frac{1}{\sqrt{\sum^F_f \left|\hat{S}_{kf}\right|^2}} - \frac{\hat{S}^2_{kf}}{\left( \sqrt{\sum^F_f \left|\hat{S}_{kf}\right|^2}\right) ^3}\right] W^{old}_{mkf} -E\left[\frac{\hat{S}_{kf}}{\sqrt{\sum^F_f \left|\hat{S}_{kf}\right|^2}} X_{kf}\right]\)
References¶
| [1] |
|
| [2] |
|